482. 3 - Разбиение
Сколькими
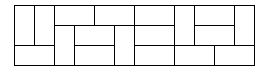
способами можно замостить 3 * n прямоугольник
при помощи 2
* 1
костей домино? Ниже приведен пример замощения такими плитками прямоугольника 3 * 12.
Вход. Состоит из нескольких тестов, заканчивающихся строкой,
содержащей -1. Каждый тест размещен в отдельной строке и содержит единственное
целое число n (0 ≤ n ≤ 30).
Выход. Для каждого
теста в отдельной строке выведите количество способов замощения.
|
Пример входа |
Пример выхода |
|
2 8 12 -1 |
3 153 2131 |
РЕШЕНИЕ
динамическое
программирование - комбинаторика
Анализ алгоритма
Обозначим через
Un количество различных
разбиений 3 * n прямоугольника
горизонтальными и вертикальными домино. Пусть Vn – количество разбиений 3 * n прямоугольника без левого нижнего угла с использованием
(3n – 1) / 2 костей домино.


Получим
следующие рекуррентные соотношения:
Un = 2Vn-1 + Un-2
Vn = Un-1 + Vn-2
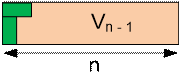


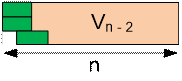
Рассмотрим
случаи для n = 1 и n = 2.
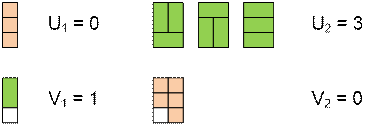
Рекуррентными
соотношениями можно воспользоваться не только для пересчета значений функций
вперед, но и назад. По условию задачи 0 ≤ n ≤ 30, следовательно нам нужны еще значения U0 и
V0. Из выведенного соотношения получим
 или
или  , откуда
, откуда 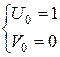
Разбиения 3*n возможны только при четном n. То есть при нечетном n значение Un равно 0. Выразим рекуррентность Un через ее же саму. Имеем:
Un = 2Vn-1 + Un-2
= 2 * (Un-2 + Vn-3) + Un-2 = 3 * Un-2 + 2 * Vn-3
Однако из Un = 2Vn-1 + Un-2
следует Un-2 =
2Vn-3 + Un-4, откуда 2Vn-3 = Un-2 – Un-4. Подставим его
в верхнее равенство, получим:
Un = 3 * Un-2 + 2 * Vn-3 = 3 * Un-2 + Un-2
– Un-4 = 4 * Un-2 – Un-4
То есть
Un = 4 * Un-2 – Un-4
Пример
Значения Un и Vn для малых n приведем
в таблице:
Реализация алгоритма
В массивах u и v
будем вычислять значения Un
и Vn.
int u[31], v[31];
Вычисляем значения
Un и Vn (n = 0, 1,
…, 30) согласно приведенным выше рекуррентным формулам.
u[0] = v[1] = 1;
u[1] = v[0] = 0;
for(n = 2; n <= 30; n++)
{
u[n] = 2 * v[n-1] + u[n-2];
v[n] = u[n-1] + v[n-2];
}
Для каждого
входного значения n выводим u[n].
while(scanf("%d",&n),n
>= 0)
printf("%d\n",u[n]);
Реализация алгоритма – другая формула
Воспользуемся
формулой Un = 4 * Un-2 – Un-4.
#include <stdio.h>
int n, u[31];
int main(void)
{
u[0] = 1; u[2] = 3;
for(n = 4; n
<= 30; n+=2)
u[n] = 4 * u[n-2] - u[n-4];
while(scanf("%d",&n),n
>= 0)
printf("%d\n",u[n]);
return 0;
}
Java реализация
import java.util.*;
public class Main
{
public static int MAX = 31;
static int u[] = new int[MAX];
static int v[] = new int[MAX];
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
u[0] = v[1] =
1;
u[1] = v[0] =
0;
for(int n = 2; n < MAX; n++)
{
u[n] = 2 *
v[n-1] + u[n-2];
v[n] = u[n-1] + v[n-2];
}
int n = con.nextInt();
while(n >=
0)
{
System.out.println(u[n]);
n = con.nextInt();
}
}
}



